Moore's Law
I’ve always been skeptical of many of the claims that people who are pro-Singularity have made regarding Moore’s Law.
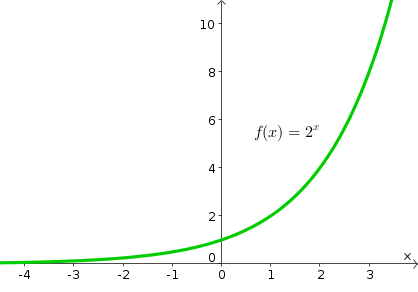
The main basis of my skepticism lies in the fact that there isn’t really anything that grows exponentially ad infinitum.
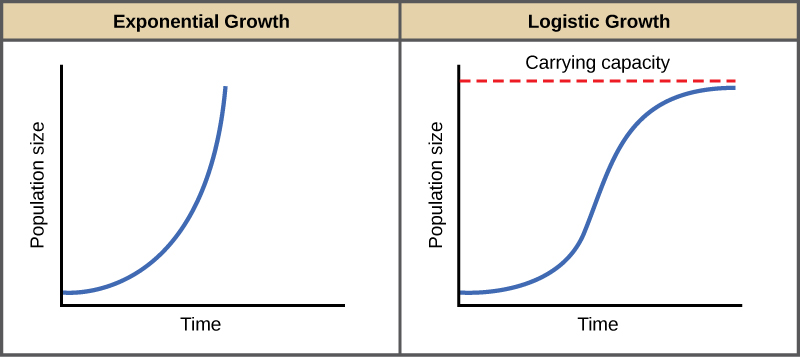
© Jun 21, 2013 OpenStax College. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 3.0 license.
Under this license, any user of this textbook or the textbook contents herein must provide proper attribution as follows:
The OpenStax College name, OpenStax College logo, OpenStax College book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the creative commons license and may not be reproduced without the prior and express written consent of Rice University. For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Environmental Limits to Population Growth. OpenStax CNX. Jun 21, 2013 http://cnx.org/contents/79ebaf1a-0e1a-4efb-9712-9bb41919a17d@4
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution:
Download for free at http://cnx.org/contents/79ebaf1a-0e1a-4efb-9712-9bb41919a17d@4
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution:
Download for free at http://cnx.org/contents/79ebaf1a-0e1a-4efb-9712-9bb41919a17d@4
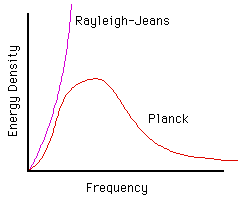
The Rayleigh-Jeans Law predicts infinite energies at very high frequencies (the ultraviolet catastrophe). Planck realized this makes no physical sense and birthed quantum mechanics.
graph from Ultraviolet Catastrophe Explanation
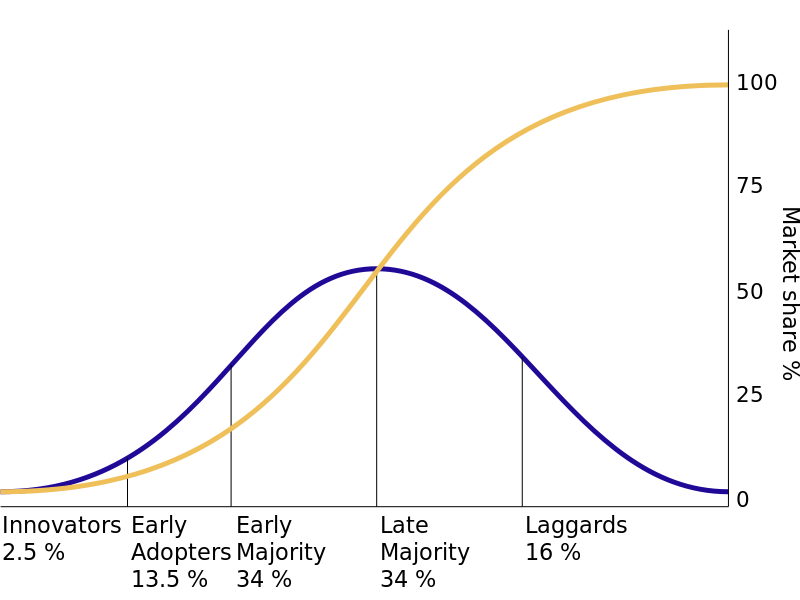
The diffusion of innovations according to Rogers. With successive groups of consumers adopting the new technology (shown in blue), its market share (yellow) will eventually reach the saturation level. In mathematics, the yellow curve is known as the logistic function. The curve is broken into sections of adopters.
Just like how in the 19th century, Verhulst realized that Malthus had oversimplified how fast the world population would grow and how catastrophic the situation would be when the population growth rate started outstripping the ability to grow food, I think John Markoff is similarly correct about the ultimate fate of Moore’s Law. It doesn’t mean that there won’t be some massively disruptive IT advance occurring in the future (Markoff is betting on augmented reality) but it certainly won’t be the result of simply packing more and more transistors onto a chip.
(via Could the End of Moore’s Law Be Near? If so, What’s Next? • • Irving Wladawsky-Berger)